Problem 10 Project euler Solution with python

Hello friends today I have solved problem 10 on project Euler and I am here to share it with you. Let's first see the question and then we will see the solution.

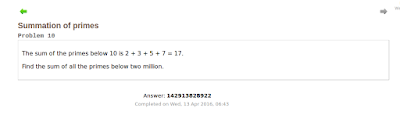
Summation of primes

The sum of the primes below 10 is 2 + 3 + 5 + 7 = 17.
Find the sum of all the primes below two million.?

My first attempt to solve this problem was to use the sieve function which I have written for  Problem 7 and extend it for generating the required solution.

But what I saw was that my solution took around 1.5 seconds to execute. I was not satisfied with the result and wanted more faster solution. Surfing on internet I found Sieve of Atkins, which most people suggested for better result.

But what I found was that Sieve of Eratosthenes had better execution time compared with the Atkin's Sieve. So obviously I have finalized the solution with the Sieve of Eratosthenes.

Program

Program written using Sieve of Eratosthenes is as follows:
If you want to understand this program search on your favorite search engine for Sieve of Eratosthenes and take some time to read it. You will for sure understand the program. After you have read the program, to understand it better, take some example and iterate manually.

If you want to download the program then you can download it from  Github Gist

Next I will also show you the Sieve of Atkins program I have written. But the original from which I have derived my program is available on Github - Sieve of Atkin.
The program is as follows:

#http://radiusofcircle.blogspot.com

#time module for calculating time
import time,math

#Time at the start of execution
start =time.time()

#Sieve of Atkins
#https://en.wikipedia.org/wiki/Sieve_of_Atkin
def sieve_of_atkins(limit):
 #Initial primes
 primes = [2,3]
 sieve = [False]*(limit+1)
 testingLimit = int(math.sqrt(limit))+1
 
 #For loop for generating x, y
 for x in xrange(testingLimit):
  for y in xrange(testingLimit):
   
   #n = 4x^2+y^2
   n = 4*int(x**2)+int(y**2)
   if n <= limit and (n%12 ==1 or n%12 ==5):
    sieve[n] = True
   
   #n = 3x^2+y^2
   n = 3*int(x**2)+int(y**2)
   if n<= limit and (n%12 == 7):
    sieve[n] = True
   
   #n = 3x^2-y^2
   n = 3*int(x**2) - int(y**2)
   if n<= limit and x > y and n%12 == 11:
    sieve[n] = True

 #for loop to remove all the multiples of primes
 for i in xrange(5,testingLimit):
  if sieve[i]:
   index = i**2
   while index < limit:
    sieve[index] = False
    index += i

 #for loop to create prime numbers list
 for i in xrange(2,len(sieve)):
  if sieve[i]:
   primes.append(i)
 return primes

#Printing the output
print sum(sieve_of_atkins(2000000))

#Time at the end of execution
end = time.time()

#total time for execution
print end-start

This program had an execution time of around 2.48 seconds which is greater than the execution time required for sieve of Eratosthenes.

If you want to understand the above program then it is better to first understand the algorithm of Sieve of Atkins and then you will be good to go. If you want to some sources where you can learn are as follows:

Sieve of Atkin Explanation

Primality Testing by Shiv

Python Sieve of Atkins Algorithm

Last but not the least: Wikipedia - Sieve of Atkins

Output

Answer:  142913828922
Execution time:  1.47674107552seconds
Output:

Project Euler Problem 10 Output

Project euler problem 10 with solution

Summary

Even though this program had execution time greater than 1 second, I didn't bother because the number was 2 million which needed a lot of computation. But I have obtained the solution within 2-4 seconds for both the programs. Also I have learned something new from this problem and I am satisfied.

I haven't explained any part of the code because it is well commented and also you can take it as an exercise where you will have to decode the code in human language. If you have any doubt or didn't understand anything then please do comment in the comment box below and I will be glad to help you.

Please don't hesitate to comment if I have made any typo or if you want me to add any extra thing. Please Please do share your program, if your program has a different approach or if it run much faster than any of the programs I have written.

You can also contact me if you want to.

Thank you. Have a nice day😃.