Problem 60 Project Euler Solution with python

Prime pair sets

The primes 3, 7, 109, and 673, are quite remarkable. By taking any two primes and concatenating them in any order the result will always be prime. For example, taking 7 and 109, both 7109 and 1097 are prime. The sum of these four primes, 792, represents the lowest sum for a set of four primes with this property.
Find the lowest sum for a set of five primes for which any two primes concatenate to produce another prime.

This problem is just a brute force problem. If you have come here because you don't know the limit upto which you will have to generate the prime numbers then go ahead and try with 10,000. When I first started solving the problem I chose 1 million(because most of the problems on projectEuler have this limit), but it took very long for the computer to find the solution. After searching on the internet then I found many people choosing 10,000 so I have changed my input from 1 million to 10000 and the output was fast.

Here goes my algorithm.

We will generate prime numbers upto 10000(Assumed) using Sieve of Erotosthenes.

Take the first number from the prime numbers list, let it be a
then take the second number the prime numbers list, let it be b . Remember that b > a.

Check if ab & ba are primes, if they are primes, then take the third number from the prime numbers list, let it be c. Remember that c > b.

Check if ac, ca, bc, ca are all primes. If they are primes then take a fourth number from the prime numbers list, let it be d. Remember that d > c.

Check if ad, da, bd, db, cd, dc are all primes. If they are all primes then take the fifth number from the prime numbers list, let the number be e. Remember that e > d.

Now check if ae, ea, be, eb, ce, ec, de, ed are all primes. If they are all primes then find a + b + c + d + e.

Now you might have got confused on why I am checking the primality of ab, ba, ac, ca .....

To understand this we will have to go back to Permutations and Combinations.

We have 5 numbers, then the number of ways of forming 2 digit numbers are ⁵P₂ = 20 and if you write them then you will get the above permutations.

Hope you have understood the concept.

Program

File: pep60.py ------------------------- # http://radiusofcircle.blogspot.com # time, random, math modules import time, random, math # start of program start = time.time() # Sieve of Erotosthenes # One of the best algorithm to generate prime numbers # https://en.wikipedia.org/wiki/Sieve_of_Eratosthenes def sieve(n): is_prime = [True]*n is_prime[0] = False is_prime[1] = False is_prime[2] = True # even numbers except 2 have been eliminated for i in xrange(3, int(n**0.5+1), 2): index = i*2 while index < n: is_prime[index] = False index = index+i prime = [2] for i in xrange(3, n, 2): if is_prime[i]: prime.append(i) return prime # Miller–Rabin primality test # One of the best algorithm to check if the given number if prime # https://en.wikipedia.org/wiki/Miller%E2%80%93Rabin_primality_test # Algorithm: http://bit.ly/2drtk0x def is_prime(n, k = 3): if n < 6: # assuming n >= 0 in all cases... shortcut small cases here return [False, False, True, True, False, True][n] elif n % 2 == 0: # should be faster than n % 2 return False else: s, d = 0, n - 1 while d % 2 == 0: s, d = s + 1, d >> 1 # A for loop with a random sample of numbers for a in random.sample(xrange(2, n-2), k): x = pow(a, d, n) if x != 1 and x + 1 != n: for r in xrange(1, s): x = pow(x, 2, n) if x == 1: return False # composite for sure elif x == n - 1: a = 0 # so we know loop didn't continue to end break # could be strong liar, try another a if a: return False # composite if we reached end of this loop return True # probably prime if reached end of outer loop # A function to find all the combinations of the given two numbers # and check if they are prime using the Rabin miller def comb(a, b): len_a = math.floor(math.log10(a))+1 len_b = math.floor(math.log10(b))+1 if is_prime(int(a*(10**len_b)+b)) and is_prime(int(b*(10**len_a)+a)): return True return False # finding out the primes upto 10000 primes = sieve(10000) # problem solution def prime_pairs(): # a is first number for a in primes: # b is second number for b in primes: # check if b is less than a if b < a: continue # check if a and b satisfy the condition if comb(a, b): # c is the third number for c in primes: # check if c is less than b if c < b: continue # check if a,c and b, c satisfy the condition if comb(a, c) and comb(b, c): # d is the fourth number for d in primes: # check if d is less than c if d < c: continue # check if (a,d), (b,d) and (c,d) satisfy the condition if comb(a, d) and comb(b, d) and comb(c, d): # e is the fifth prime for e in primes: # check if e is less than d if e < d: continue # check if (a, e), (b, e), (c, e) and (d, e) satisfy condition if comb(a, e) and comb(b, e) and comb(c, e) and comb(d, e): return a+b+c+d+e # run the function and print the output print prime_pairs() # end of program end = time.time() # total time for program execution print end-start

Don't get scared by seeing the size of the program. It is very simple.

Here goes the explanation of the program:

Line 10 - 22: This is the Sieve of Erotosthenes. It is a very great algorithm to find the prime numbers upto a given number. You can learn more about the Sieve of Erotosthenes on Wiki. You can also see the explanation of the program code given here: Problem 35 Project Euler Solution with python. . We have modified a little bit of that program but the core concept in the same.

You can also learn more about sieve from:
Prime Sieve
Geeks of Geeks Sieve of Erotosthenes

Line 34 - 56: This is Rabin Miller Primality test. This function can be used to find if the given number is prime or not. This function will be useful when we will find if the permutations of the given number is prime or not. You can see more about Rabin Miller from here:
Miller Rabin Primality Test - Wiki
Algorithm Rabin Miller

We could have used this function to generate all the prime numbers upto 10000, but the problem is that this function is slow to generate the prime numbers when compared to Sieve of Erotosthenes. But this function does its job well when it is assigned to check if the given number is prime.

Line 60 - 66: This function comb will find all the permutations of the given number. This function will not do any string to integer, integer to string conversions. It will only do the math. I suggest you to work out for your own on how this function works. It is fun.

Rest of the code has already been explained in the algorithm section. I suggest you to take some random prime numbers and plug them in the place of the variables in the program and then you will for sure understand how the program is working very easily.

As always you can download the program from Github Gist pep60.py

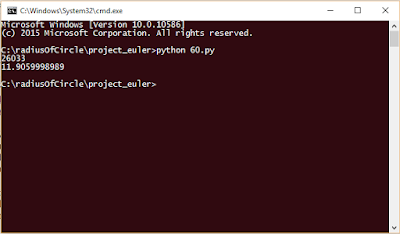
Output

Summary

Even though this problem has got 20% rating I don't think that this problem is not worth giving that rating. This problem is very easy once you will be able to guess the limit upto which you will have to find the prime numbers. This took very long for me. But no problem I was able to solve the problem with the help of internet community with confidence. A nice problem in one way, it tests the way you will understand the problem and try to crack it. Even though I was able to solve this problem in around 12 seconds, there should be some scope for improvement.

As always if you have any doubt or didn't understand anything then you can comment in the comment box below and I will be glad to help you.

If you have any suggestion(s) or have found any typo or if you have any new program or better program then please comment in the comment box.

You can also contact me.

Thank you. Have a nice day.😃

Problem 11 Project Euler Solution with python

Largest product in a grid In the 20×20 grid below, four numbers along a diagonal line have been marked in red. 08 02 22 97 38 15 00 40 00 75 04 05 07 78 52 12 50 77 91 08 49 49 99 40 17 81 18 57 60 87 17 40 98 43 69 48 04 56 62 00 81 49 31 73 55 79 14 29 93 71 40 67 53 88 30 03 49 13 36 65 52 70 95 23 04 60 11 42 69 24 68 56 01 32 56 71 37 02 36 91 22 31 16 71 51 67 63 89 41 92 36 54 22 40 40 28 66 33 13 80 24 47 32 60 99 03 45 02 44 75 33 53 78 36 84 20 35 17 12 50 32 98 81 28 64 23 67 10 26 38 40 67 59 54 70 66 18 38 64 70 67 26 20 68 02 62 12 20 95 63 94 39 63 08 40 91 66 49 94 21 24 55 58 05 66 73 99 26 97 17 78 78 96 83 14 88 34 89 63 72 21 36 23 09 75 00 76 44 20 45 35 14 00 61 33 97 34 31 33 95 78 17 53 28 22 75 31 67 15 94 03 80 04 62 16 14 09 53 56 92 16 39 05 42 96 35 31 47 55 58 88 24 00 17 54 24 36 29 85 57 86 56 00 48 35 71 89 07 05 44 44 37 44 60 21 58 51 54 17 58 19 80 81 68 05 94 47 69 28 73 92 13 86 52 17 77 04 89 55 40 04 52 08 83 97 35 99 16 07

RADIUS OF CIRCLE

Search This Blog