Smallest multiple
2520 is the smallest number that can be divided by each of the numbers from 1 to 10 without any remainder.
What is the smallest positive number that is evenly divisible by all of the numbers from 1 to 20?
To be simple the question asked was to find the LCM(Least Common multiple) of numbers from 1 to 20.
If we use Common Factors Grid method to find the value manually on paper, it can easily be found out.
But to write a program to find the LCM of two or more numbers you should be knowing Euclid Algorithm. But Euclid Theorem was designed for only two numbers. Let us assume that we will have to find LCM of 3 numbers n1,n2,n3. As LCM is both assertive and commutative we can write LCM(n1,n2,n3) = LCM(LCM(n1,n2),n3). This is what I have used in the program.
Also if you don't know what Euclid Algorithm is then Please check out Wikihow - Ways to Find the LCM of two numbers.
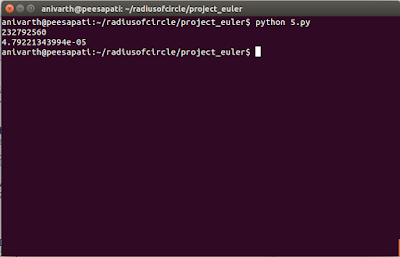
The program is fast and it just took me 5.19752502441e-05 seconds.
I think this program is pretty simple and there is nothing to explain. So I am not explaining anything.
One thing I want to mention is the possibility to use the reduce function. Instead of using for loop on line31, you can use reduce function.
If you want to download the program then you can download it from Github Gist
I would like to thank the StackOverflow community and Wikihow which helped me framing the program for this problem.
Least common multiples of 3 or more
How to find the Largest Common multiple of two numbers
Finally as all the code is neatly commented I have not explained anything. But if you have any doubt or didn't understand anything, please do comment in the comment box below and I will be glad to help you.
Please don't hesitate to comment if you want me to add any extra thing or if I have made any typo.
You can also contact me if you want to.
Thank you. Have a nice day☺️.
What is the smallest positive number that is evenly divisible by all of the numbers from 1 to 20?
To be simple the question asked was to find the LCM(Least Common multiple) of numbers from 1 to 20.
If we use Common Factors Grid method to find the value manually on paper, it can easily be found out.
But to write a program to find the LCM of two or more numbers you should be knowing Euclid Algorithm. But Euclid Theorem was designed for only two numbers. Let us assume that we will have to find LCM of 3 numbers n1,n2,n3. As LCM is both assertive and commutative we can write LCM(n1,n2,n3) = LCM(LCM(n1,n2),n3). This is what I have used in the program.
Also if you don't know what Euclid Algorithm is then Please check out Wikihow - Ways to Find the LCM of two numbers.
Program
So the program which I wrote is as follows:The program is fast and it just took me 5.19752502441e-05 seconds.
I think this program is pretty simple and there is nothing to explain. So I am not explaining anything.
One thing I want to mention is the possibility to use the reduce function. Instead of using for loop on line31, you can use reduce function.
If you want to download the program then you can download it from Github Gist
Output
Summary
Solving this problem on paper was easy. But converting it to a program took some time for me. I think this problem was easy if you knew Euclid Algorithm, which was not so in my case. So I had to understand the concepts behind the algorithm and this problem became easy for me.I would like to thank the StackOverflow community and Wikihow which helped me framing the program for this problem.
Least common multiples of 3 or more
How to find the Largest Common multiple of two numbers
Finally as all the code is neatly commented I have not explained anything. But if you have any doubt or didn't understand anything, please do comment in the comment box below and I will be glad to help you.
Please don't hesitate to comment if you want me to add any extra thing or if I have made any typo.
You can also contact me if you want to.
Thank you. Have a nice day☺️.