Skip to main content

Problem 6 Project Euler Solution with python

Sum square difference

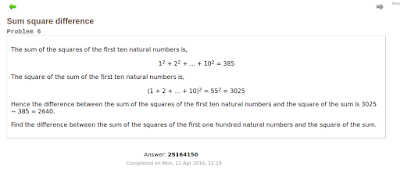
The sum of the squares of the first ten natural numbers is,
12 + 22 + ... + 102 = 385
The square of the sum of the first ten natural numbers is,
(1 + 2 + ... + 10)2 = 552 = 3025
Hence the difference between the sum of the squares of the first ten natural numbers and the square of the sum is 3025 − 385 = 2640.
Find the difference between the sum of the squares of the first one hundred natural numbers and the square of the sum?

 So as usual I will show you the first program which I wrote for this one, and also the improved program so that you can understand it easily.

 To be frank both the programs are having approximately the same time of execution for the given set of first hundred numbers. So I had to try for first one million numbers and I found that the improved program was having more run time than that of the first program.

 Thus we can say that the first program which I wrote was better than the improved version.

Program

The first program I wrote was:
As you can see it is pretty simple and I think there is no need for explanation.
If you want to download this program then you can download it from Github gist.

 The improved version(Even though it took more execution time, as it was the second program I wrote I am calling it improved version) which I told you is as follows:

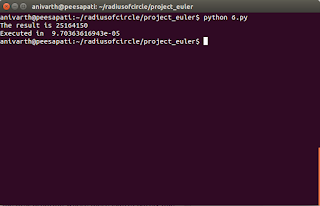
#http://radiusofcircle.blogspot.com
import time

#Time at the start of execution
start = time.time()

#sum of squares of natural numbers
sum1 = sum(map(lambda x: x**2, range(1,101)))

#square of sum of natural numbers
sum2 = sum(range(1,101))**2

#result
result = sum2 - sum1

#printing the result
print result

#Time at the end of execution
end = time.time()

#printing the execution time
print end-start
To understand this program one has to read

 In the first sum(sum1) we have used lambda expression combined with map function to take each and every element in the list and then convert it into its square. Finally using the sum function I have added all the values in the list.
In a similar way we have used the sum function to find the sum of natural numbers from 1 to 100 and stored the value in sum2.

Output


Summary

 I think because of using lot of functions in the second program, the execution time is more when compared to the first program where there is(are) barely one function(s) used.

 I have not explained the program because the program is well commented. But if you have any doubt or didn't understand anything then please do comment in the comment box below and I will be glad to help you.

 Please don't hesitate to comment in the comment box below if I have made any typo or if you want me to add any extra thing in the program.

 You can also contact me if you want to.

 Thank you. Have a nice day☺️.
Labels:

Popular posts from this blog

Project Euler Problem 67 Solution with Python

Maximum path sum II By starting at the top of the triangle below and moving to adjacent numbers on the row below, the maximum total from top to bottom is 23. 3 7 4 2 4 6 8 5 9 3 That is, 3 + 7 + 4 + 9 = 23. Find the maximum total from top to bottom in triangle.txt (right click and 'Save Link/Target As...'), a 15K text file containing a triangle with one-hundred rows.
Read more

Problem 60 Project Euler Solution with python

Prime pair sets The primes 3, 7, 109, and 673, are quite remarkable. By taking any two primes and concatenating them in any order the result will always be prime. For example, taking 7 and 109, both 7109 and 1097 are prime. The sum of these four primes, 792, represents the lowest sum for a set of four primes with this property. Find the lowest sum for a set of five primes for which any two primes concatenate to produce another prime. This problem is j u st a brute force problem. If you have come here because you don't know the limit upto which you will h ave to gener ate the prime numbers t hen go ahe ad and t r y with 10,000 . When I first start ed solving the problem I chose 1 million(beca use most of the problem s on project E uler have this limit ), but it took very long for the computer to fin d the solution. After searching on the internet then I found many people choosing 10, 000 so I have changed my in put f rom 1 million to 10000 and the output was f ast. He...
Read more

Project Euler Problem 66 Solution with python

Diophantine equation ¶ Consider quadratic Diophantine equations of the form: $$ x^{2} – Dy^{2} = 1 $$ For example, when $D = 13$, the minimal solution in $ x $ is $ 649^{2} – 13 \times 180^{2} = 1 $ It can be assumed that there are no solutions in positive integers when $ D $ is square. By finding minimal solutions in $ x $ for $ D = {2, 3, 5, 6, 7} $, we obtain the following: $$ 3^{2} – 2×2^{2} = 1 $$ $$ 2^{2} – 3×1^{2} = 1 $$ $$ 9^{2} – 5×4^{2} = 1 $$ $$ 5^{2} – 6×2^{2} = 1 $$ $$ 8^{2} – 7×3^{2} = 1 $$ Hence, by considering minimal solutions in $ x $ for $ D ≤ 7 $, the largest $ x $ is obtained when $ D = 5 $. Find the value of $ D ≤ 1000 $ in minimal solutions of $ x $ for which the largest value of $ x $ is obtained.
Read more