Problem 37 Project Euler Solution with python

Truncatable primes

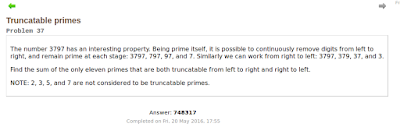
The number 3797 has an interesting property. Being prime itself, it is possible to continuously remove digits from left to right, and remain prime at each stage: 3797, 797, 97, and 7. Similarly we can work from right to left: 3797, 379, 37, and 3.
Find the sum of the only eleven primes that are both truncatable from left to right and right to left.

NOTE: 2, 3, 5, and 7 are not considered to be truncatable primes.

I would like to call this problem an extension for Problem 35 for which we have already written a solution. You can see the solution from here: Problem 35 Project Euler Solution with python

Now with this problem, it just took me a few minutes to write the code.But the real problem before I started writing the code was the upper bound. I have searched on internet for finding the upper bound, but couldn't get any, so I have assumed the upper bound to be 1 million. I don't have any reason for that. It's just an assumption by me.

On Truncatable primes, I don't know if this can give us the logical upper bound, if it can then please do share with me the same. Not only this, you can also share your own theory, so that we can help the community.

I will explain you the algorithm used by me in the program and I will also explain you the code.

Similar to Problem 35 I have Sieved to get primes under 1 million. I took each and every prime and then found if it is right truncatable. After I have found a list of all the right truncatable primes under 1 million. They were around 70 of them. This was a very small list. I took each and every element of right truncatable numbers and found whether the same numbers were left truncatable.

But when I was writing the code, I didn't want to check each and every prime numbers(There were around 78498 primes) for right truncatability test. So I used the same code again from problem 35, where if the numbers had multiples of 2 or 5 in their digits they can be eliminated. Even though this worked faster, it had its own cons. It eliminated all the numbers like, 23, 29, 53, 59... The problem was obvious because we have asked the program to eliminate all the numbers which had multiples of 2 or 5 in their digits.

The only solution to solve this problem was to remove the first digit from our consideration when we check the prime number. Think on your own, why only leaving the first digit debugged the program.

That is it. You can have a insight of the program to understand the algorithm in pythonic language. This time I have also added explanation for the code, you can see that below the program.

Program

As you can see most of the code is from problem 35, we just have made a few modifications to the same. I am not going to explain you about the Sieve of Erotosthenes which we have used earlier.

primes = sieve(1000000)

Using the above command, I have stored the prime numbers below 1 million in a variable primes.

solution = []

I have created an empty solution set to store the values of the primes which are both truncatable from right and left.

for prime in primes:

I have started a for loop to loop through each and every prime number.

flag = True

As the iteration starts and the first prime number enters into the loop, we are assuming that the current prime number is both truncatable from left and right. If in the future tests if it is found that it is not truncatable from left and right then we will flag = False.

number = prime

We are making a duplicate of the prime so that it can be used for our calculations. Because if we had used the same prime variable for our calculations then it would make the loop infinite.

mul = 10**(len(str(number))-1)
number = (number-(number/mul)*mul)/10

These two statements are for preparing the number to be checked if the number has any digits which are multiples of 2 and 5. We are not considering the first digit the reason for which has been discussed earlier. To understand these statements, let us consider a number 313, which when converted to a string will be '313', whose length is 3. So the value of mul for 313 will be 10**(3-1) = 10**2 = 100. In the next statement or command, what ever you might call it, value of number will become (313-(313/100)*100)/10. As we know that in python division with both integer numerator and integer denominator result will be a quotient without any decimals. So the value of above equation will become (313-(3)*100)/10 = (313-300)/10 = (13/10) = 1. You might have got confused with the last division 13/10. We are doing this because if the last digit had any even number or 5 then it would not have been a prime number at all.

while number:
 if (number%10) % 2 == 0 or (number%10) %5 == 0:
  flag = False
  break
 number = number/10

Value of number variable is 1 and the above while loop iterations are very simple that you can understand them very easily yourself. The only thing I want to stress is that, if the number is found to have any digits with 5 or multiples of 2 then flag = False.

if flag:

This condition will check if the number has passed the above digits test, if yes the number can be tested for trucatability, otherwise it will not be sent to trash😊.

number = prime/10

Now again consider the same number 313, as we know that this number is a prime it is not necessary for us to check again for its primaity. So we are starting with 31 i.e. 313.

solution.append(prime)

We are assuming that this prime number is right truncatable and so we are adding it to the solution set.

while number:
 if number not in primes:
  solution.remove(prime)
  break
 number //= 10

An another while loop, as simple as it looks. Only important thing I want to share is that if the number is found not to be right truncatable then the number is removed from the solution set.

sol = solution[4:]

Finally after the looping is over we are presented with a list which has 2,3,5,7 also. So we will delete all these numbers from that list and make a copy of the same for looping further.

for i in sol:
 number = i
 while number:
  mul = 10**(len(str(number))-1)
  number = number - (number/mul)*mul
  if number not in primes and number != 0:
   solution.remove(i)
   break

This for loop works similar to the above used for loop, but it has some difference, in this for loop we are taking the number cutting it from front and then checking for its primality. I mean we are checking for left truncatability. I will just explain you the if statement. We are checking the number of its primality and also if it is not equal to 0, because if we had not checked if the number is not zero then the if statement will get executed, even if the number is both truncatable.

As we have done in the previous code, you can assume a prime number which seems to have qualified the right truncatability and replace all the variables in the above for loop, you will understand everything easily. One important thing is that, if the number is right truncatable number and is not found to be left truncatable, then we will remove it from the solution set. So finally our standard answer will be with the solution set itself not the sol set.

Thats it, I don't think I will have to explain the final printing statement also😄.

You can download the above source code from Github Gist pep37.py

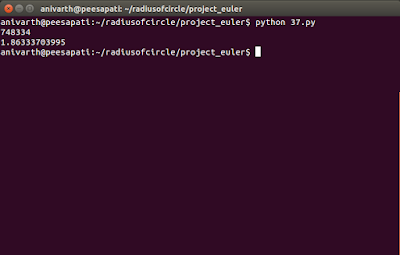
Output

Answer:  748334
Execution time: 1.86333703995 seconds
Output:

Project Euler problem 37 output

Project Euler Problem 37 with answer

Summary

Writing this code was easy and simple, but it took some time for finding the left truncatable test and also assuming the upper bound. Anyways I am satisfied with the program. I think there is a scope for improvement and you can even optimize the code. As I was satisfied I have posted it here. Today I am really satisfied not for a slower execution time but because after so many days I have explained each and every part of the code perfectly.

As always if you have any doubt or didn't understand anything, then you can comment in the comment box below and I will be glad to help you.

Please do comment if you have found any typo, or Grammar mistake, or if you have different program, or if you have a better program, or if you have any suggestion. I will be glad to view your comment.

You can also contact me.

Thank you. Have a nice day😃.

You can see the sequences of Left truncatable numbers from : A024785 
Right Truncatable numbers: A024770 
Both Truncatable numbers: A020994 
More about Truncatable numbers: Truncatable primes