Triangular, pentagonal, and hexagonal
Triangle, pentagonal, and hexagonal numbers are generated by the following formulae:
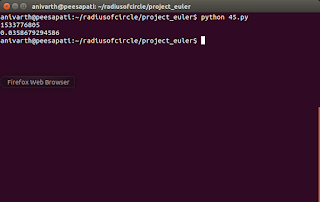
It can be verified that T285 = P165 = H143 = 40755.
Find the next triangle number that is also pentagonal and hexagonal.
| Triangle | Tn=n(n+1)/2 | 1, 3, 6, 10, 15, ... | ||
| Pentagonal | Pn=n(3n−1)/2 | 1, 5, 12, 22, 35, ... | ||
| Hexagonal | Hn=n(2n−1) | 1, 6, 15, 28, 45, ... |
Find the next triangle number that is also pentagonal and hexagonal.
A very easy problem if you know the condition to check if the given number is Pentagonal Number and Hexagonal Number. We have used while loop to arrive at the solution.
There is no big algorithm used in this program. You can go see the program and understand it simply.
Program
You can download the above source code from Github Gist pep45.py
Output
Summary
It just took a few seconds for me to write the program. I am satisfied with the solution. I have not tried to optimize the code to improve the performance because the program is very fast anyways. I think there is some scope to improve the present solution. You can improve the program if you want to. Please do share it with me if you have written a new solution.
As always you can comment in the comment box below if you have any doubt or didn't understand anything. I will be glad to help you.
Please do comment in the comment box below if you have found any typo or have a different program or a better program or have any suggestion. I will be very happy to view each of them.
You can also contact me.
Thank you. Have a nice day😃!