Problem 46 Project Euler Solution with python

Goldbach's other conjecture

It was proposed by Christian Goldbach that every odd composite number can be written as the sum of a prime and twice a square.

9 = 7 + 2×1²
15 = 7 + 2×2²
21 = 3 + 2×3²
25 = 7 + 2×3²
27 = 19 + 2×2²
33 = 31 + 2×1²

It turns out that the conjecture was false.
What is the smallest odd composite that cannot be written as the sum of a prime and twice a square?

Algorithm for this program is simple. We will start with number 3. As we don't know the upper limit, we will use a while loop. Question states that the number on the left hand side is a composite odd number. Now let us consider the equation given in the question as follows:

number = prime + 2 × some_number2

⇒ some_number = ((number-prime)/2)1/2

In the above equation for some_number to be a positive integer there are two conditions, value of number should be greater than prime number or we can say - We can iterate with the prime numbers below number. Value of some_number((number-prime)/2) should be a perfect number.

Coming back to our program and its iterations, as 3 is a prime number we will add it to a list of prime numbers. The next odd number is 5, which is again a prime number so add it to primes list. 7 is again a prime number. 9, this is a composite number. We will take a number from [2,3,5,7](prime numbers below 9) and check for the condition - the value of (number-prime)/2 to be a perfect number. If this condition is satisfied with any of the prime numbers below 9 then the number satisfies Goldbach other conjecture. In case of 9, it satisfies the condition.

 But at some point the given number does not satisfy the condition, which is the required answer.

Program

 As already explained, in this program we have written a function is_prime to check if the number is prime or not. 

number = 3

This will be the iter for our while loop.

primes = [2]

As we are not looping through any even numbers, we will add the only even prime in the list to check for the condition. All the other primes will be added to the list further down at the while loop during iterations.

# while loop
while True:
 if is_prime(number):
  primes.append(number)
 else:
  for i in primes:
   if math.sqrt(((number-i)/2)) == int(math.sqrt(((number-i)/2))):
    break
  else:
   print number
   break

 number += 2

As per the question we only need composite odd numbers, also for our calculations we need prime numbers, so in this part of while loop we will check if the number at which we are iterating is prime or not, if it is prime then we will add it to prime number list. If the number is not a prime number i.e if it is a odd composite number, then take each and every number in the primes list(largest number in the list at any given iteration is less than the iterator) and check for the condition((number-prime)/2)

which we have discussed above. We have used for else. You should learn more about for else from google if you are not good at it. It is a good and useful concept for control flow.

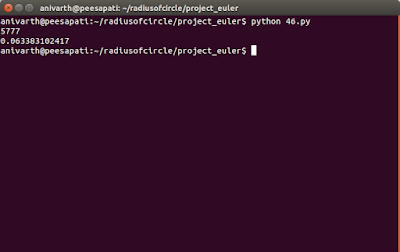
Everything else is easy. I suggest you to take an example i.e start from 3 try all the iterations upto 15(atleast), I am sure you will for sure understand the while loop(and everything else) easily.

You can download the above source code from Github Gist 46.py

Output

Answer: 5777
Execution time: 0.063383102417 seconds
Output:

Project Euler Problem 46 output

Project Euler Problem 46 with answer

Summary

This is a different problem, it demanded thinking upto infinity. We also had to break out of the loop once the solution is found. I personally liked this problem. When I first wrote a solution for this problem, execution time was around 6 seconds, then I modified the program and then the execution time dropped to 4 seconds. At the end I further modified the program a little bit and then, execution time fell down to less than 0.1 seconds. A very drastic change. I am satisfied with the program. But still there is scope for improvement. 

As always you can comment in the comment box below if you have any doubt or have not understood anything. I will be glad to help you.

Please do comment in the comment box below, if you have found any typo, or have a different program or have a better program or have any suggestion. I will be very happy to view each of them.

You can also contact me.

Thank you. Have a nice day😃! 
My References: Toying with a lesser known Goldbach Conjecture
  A lesser knon Goldbach Conjecture
Goldbach Conjecture Wikipedia