Consecutive prime sum
The prime 41, can be written as the sum of six consecutive primes:
This is the longest sum of consecutive primes that adds to a prime below one-hundred.
The longest sum of consecutive primes below one-thousand that adds to a prime, contains 21 terms, and is equal to 953.
Which prime, below one-million, can be written as the sum of the most consecutive primes?
41 = 2 + 3 + 5 + 7 + 11 + 13
This is the longest sum of consecutive primes that adds to a prime below one-hundred.
The longest sum of consecutive primes below one-thousand that adds to a prime, contains 21 terms, and is equal to 953.
Which prime, below one-million, can be written as the sum of the most consecutive primes?
A very good problem, took 2 days for me to get a very good algorithm. I am assuming that this post will be a bit long, read the whole post to understand the program better.
Before we start solving the question we will first have to understand the question properly. As some of you might think that the consecutive primes means 2,3,5,7,.... but consecutive primes also mean 3,5,7,... or 11,13,17,19,.... also. For example(given in the question), consider the longest sum of consecutive primes below one-thousand, which is equal to 953 but the sum is:
[7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89]
The consecutiveness starts from 7 but not 2 or 3. Hope you have understood the question correctly.
So we will have to find a largest sub list of consecutive prime numbers. As we know that we can create sub lists using list slicing, we can use two for loops in which the iterator in the first for loop will indicate the start and the second for loop's iterator will indicate the end. Example
primes[i:j], where primes is the list and i is the iterator of first for loop, j is the iterator of second for loop.
Consider an example. Consider the primes below 100, they are :
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97]
As you know we will start with 2 and sum up all the primes until we reach the sum less than 100,
2+3+5+7+11+13+17+19+23 = 100, At this stage(at 23) the loop will break, as we don't need any numbers whose value will make the sum greater than 100(for our present example).
In the next iteration, the maximum end we can reach will be:
3+5+7+11+13+17+19+23+29 = 127, at this stage we can break the loop for the same condition.
In next iteration, the loop will end at:
5+7+11+13+17+19+23+29 = 124, at this stage the loop will break.
In next iteration, 7+11+13+17+19+23+29 = 119, the loop breaks.
But from our above sequences we cannot see any trend, but we can come to a conclusion to reduce the number of iterations the second loop will have to forego. We can find the maximum value of the second for loop iterator, by making a conclusion.
Let us say that in a loop we will hit the sum of 100 at n, then the maximum value that the next loop will hit the sum of 100 will be at n+1.
In this way we don't need to loop till the end of the primes list.
Hope you have understood the conclusion. If not try to read the further part even if it doesn't make any sense. Finally try to understand the program. If you still don't understand the program comment or contact me. I will for sure help you.
Now we will see the algorithm step by step and I am sure this will make sense even if you are confused till now.
1) Make a list of prime numbers upto 1 million.
2) Create a variable to store length, consecutive prime sum and maximum value the second for loop iterator can take. Lets call them
length, largest, lastj respectively.3) Start a
for loop(call this loop first for loop) and the maximum value upto which it can loop will be upto the length of the prime numbers list generated in Step 14*) Start another for loop(call this loop second for loop) nested in the for loop of Step 3, and set the start value of the for loop as iterator value of first for loop added with the previous length of the largest consecutive prime sum.
5) Find the sum of the prime numbers after slicing the list with the values of the iterator. Example:
primes[i:j]6) Check if the sum of the primes in of the sub list is less than 1 million. If the value is less than 1 million then continue for Step 7, otherwise change the value of the
lastj to the value of j+1 and break the second for loop.7) Check if the sum of the primes is a prime number and if it is a prime number, then change the value of length, to the length of the list generated in Step 5 and the value of largest to the sum of the primes sub list.
8) Continue for the next iteration after this iteration is over. Finally print the value of largest to find the answer.
*We are starting with a minimum length of the previously calculated largest consecutive length because, it is unnecessary to calculate for values less than the previously known number. In fact we can start with some known number if we can prove the minimum length of the largest consecutive prime sum will be.
You can see the program and I recommend you to start with substituting some values in the variables and understand what's happening behind the scenes.
Program
sieve function
We are using prime sieve to generate prime numbers. Note that we have used the modified
sieve function, from Problem 35 Project Euler Solution with python. You can learn more about Prime sieve from here: primes = sieve(1000000)
This is the Step 1 which we have already discussed above.
lastj = len(primes)
We have used len in built method, to calculate the length of the primes list.
Line 42- Line 53 - Step 4 to Step 8
You can download the above source code from Github Gist pep50.py
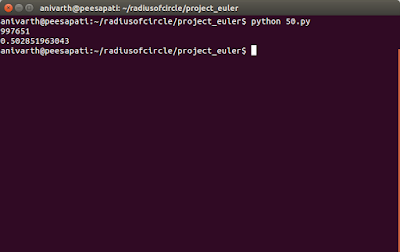
Output
Summary
Even though, this problems took a few days for me to solve, the first time I wrote a solution for this problem had an execution time of around 300 seconds, as I was not satisfied with the results and wanted a more faster solution, I started thinking about this problem in such a way that I even had a dream about this problem. Anyways at last I have completed this problem with flying colors and the present solution as you can see, runs in less than a second. One thing I want to state is that, number of iterations happening in the above program is around 600 which is far distant from 78000(approx. number of prime numbers below 1 million). I am satisfied with the solution I have written and if you know any way where we can still optimize the code then please do comment.
As always comment in the comment box below if you have any doubt or didn't understand anything. I will be glad to help you.
Please do comment in the comment box below if you have found any typo or have a better program or a different program or have a suggestion. I will be very happy to view each of them.
You can also contact me.
Thank you. Have a nice day😃!