Problem 58 Project Euler Solution with python

Spiral primes

Starting with 1 and spiralling anticlockwise in the following way, a square spiral with side length 7 is formed.

37 36 35 34 33 32 31
38 17 16 15 14 13 30
39 18 5 4 3 12 29
40 19 6 1 2 11 28
41 20 7 8 9 10 27
42 21 22 23 24 25 26
43 44 45 46 47 48 49

It is interesting to note that the odd squares lie along the bottom right diagonal, but what is more interesting is that 8 out of the 13 numbers lying along both diagonals are prime; that is, a ratio of 8/13 ≈ 62%.
If one complete new layer is wrapped around the spiral above, a square spiral with side length 9 will be formed. If this process is continued, what is the side length of the square spiral for which the ratio of primes along both diagonals first falls below 10%?

You can call this problem a continuation to the Problem 28. I simply have modified the problem 28 project euler Solution with python and have used to solve this problem.

Please have a look at the solution which I have written earlier for problem 28 to understand this solution.

The algorithm is as follows:

1) Write a function to test if the given number is prime.

2) Generate all the diagonal numbers in the spiral, For each and every new layer check if the ratio of length of prime numbers to the length of all numbers is less than 10%.

3) If the length is less than 10%, break the loop and print the square root of the last number. Otherwise continue the next iteration with step1.

We are using the square root of the number as the solution because, it will be the side length of the layer.

That's it. Please make sure you have read the solution for problem 28, otherwise this solution will be somewhat tricky for you to understand.

Program

File: pep58.py ------------------------- # http://radiusofcircle.blogspot.com # time module for calculating the execution time import time # time at the start of program execution start = time.time() def is_prime(n): """function to find if the given number is prime""" for i in xrange(3, int(n**0.5)+1, 2): if n % i == 0: return False return True # iterator for the numbers i = 0 # gap for every four iterations gap = 1 # ratio of lenght of primes to length of diagonals ratio = 1 # prime numbers on the diagonal primes = [] # all the numbers, including 1 all_numbers = [1] # While loop, to loop until we reach the last number while ratio > 0.1: for j in xrange(4): # generating the value of n for 2n+1 i += gap # generating the odd number present_number = 2*i + 1 # appending the number to all_numbers all_numbers.append(present_number) # appending to prime if the number is prime if is_prime(present_number): primes.append(2*i + 1) # changing the value of ratio at the end of loop ratio = float(len(primes))/len(all_numbers) # increasing the gap after every 4 numbers gap += 1 # printing the side length print (2*i+1)**0.5 # time at the end of the program execution end = time.time() # printing the total time of execution print end - start

is_prime function

In this function I am not checking for any even number divisibility because, only odd numbers are generated along the diagonals.

ratio = 1

At the start of the program I am assuming that the ratio will be 100%. First reason is that the while loop will not run if we are not assuming so and the second reason, after the first iteration the value of the ratio will change to the practical real value.

present_number = 2*i+1

We know that from the program, i value generated indicates the i^th odd number. So we don't need i but we need odd number. From Odd number-Wolfram, odd number will be 2*i+1.

Remaining all are simple. I am assuming that you can understand them easily.

As always you can download the source code from github gist 58.py

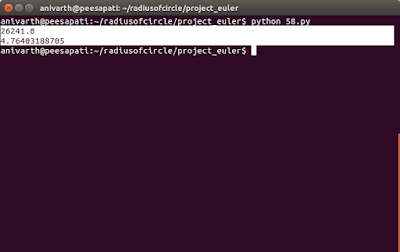
Output

Summary

As you can see, the execution time is more for this problem. The reason is that, I have used an inefficient Primality testing function. This seriously increased the execution time. I could have optimized the code by using an efficient Primality algorithm but I have left it for you. You can make some small changes and see the effect. But I am satisfied with the program which I have written. I personally liked this problem.

Please correct me and excuse me, if my grammar is wrong or in an ambiguous way.

Comment in the comment box below, if you have any doubt or haven't understood anything. I will be glad to help you.

Please do comment in the comment box below, if you have found any typo or have a better or different program or have a suggestion. I will be glad to view each of them.

You can also contact me.

Thank you. Have a nice day😃!

RADIUS OF CIRCLE

Search This Blog