Skip to main content

Check Pythagorean triplet using Matlab

Program

We know that the Pythagorean is an equation which satisfies the following condition:
a2 + b2 = c2
Write a program with Matlab, which takes the user input of the numbers and checks if the above condition is satisfied. If the condition is satisfied then display the success to the user.
Image of a right angle triangle - pythagorean triplet theorem - (c) Wikipedia
Right angle triangle

Solution

We take the user input and then use the if else statement to check if the user has entered three number which are in accordance to the Pythagorean theorem and display the success using the fprintf in Matlab.
Some of the concepts you need to know to solve the above problem are as follows:
1) User input using input function
2) if else statement in Matlab
3) fprintf in Matlab

Program


1
2
3
4
5
6
7
8
9
a = input('Enter length of Opposite side(a): ');
b = input('Enter the length of Adjacent side(b): ');
c = input('Enter the length of Hypotenuse(c): ');

if a^2 + b^2 == c^2
    fprintf('Thats a pytagorean triplet\n');
else
    fprintf('Sorry not a pythagorean triplet\n');
end
I have saved this file as pythagorean.m on my local computer.

Explanation

I have asked the user to input their values for the length of the sides of the triangle and using the if else I have checked the Pythagorean condition and if the condition is satisfied then display the user that the triplet entered is Pythagorean triplet. Otherwise(else), display not a Pythagorean triplet.

Try it yourself

1) In the above program even if the user enters negative values it checks the values for the pythagorean triplet. But this is not in the real case. Write a program such that if the user enters negative values then display that they have entered invalid numbers. Comment your program in the comment box below.

Input/output

Check if the user has entered pythagorean triplet, using Matlab - Matlab session
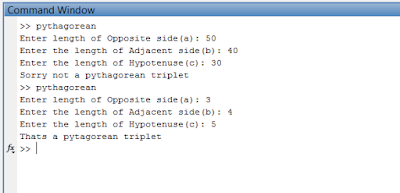Check the Pythagorean triplet using Matlab

Final Note

As always please do contact me if you have any doubt, suggestion, or did not understand anything. You can also comment in the comment box below and I will respond to you as soon as possible. You can contact me from here: Contact me
The above program was high lighted using hilite.me
Keywords: pythagorean. triplet
Labels:

Popular posts from this blog

Project Euler Problem 62 solution with python

Cubic permutations ¶ The cube, 41063625 (3453), can be permuted to produce two other cubes: 56623104 (3843) and 66430125 (4053). In fact, 41063625 is the smallest cube which has exactly three permutations of its digits which are also cube. Find the smallest cube for which exactly five permutations of its digits are cube.
Read more

Project Euler Problem 67 Solution with Python

Maximum path sum II By starting at the top of the triangle below and moving to adjacent numbers on the row below, the maximum total from top to bottom is 23. 3 7 4 2 4 6 8 5 9 3 That is, 3 + 7 + 4 + 9 = 23. Find the maximum total from top to bottom in triangle.txt (right click and 'Save Link/Target As...'), a 15K text file containing a triangle with one-hundred rows.
Read more

Problem 43 Project Euler Solution with python

Sub-string divisibility The number, 1406357289, is a 0 to 9 pandigital number because it is made up of each of the digits 0 to 9 in some order, but it also has a rather interesting sub-string divisibility property. Let d 1 be the 1 st digit, d 2 be the 2 nd digit, and so on. In this way, we note the following: d 2 d 3 d 4 =406 is divisible by 2 d 3 d 4 d 5 =063 is divisible by 3 d 4 d 5 d 6 =635 is divisible by 5 d 5 d 6 d 7 =357 is divisible by 7 d 6 d 7 d 8 =572 is divisible by 11 d 7 d 8 d 9 =728 is divisible by 13 d 8 d 9 d 10 =289 is divisible by 17 Find the sum of all 0 to 9 pandigital numbers with this property. One might write a simple solution using direct if else statements for this problem. Using if else statements, the execution time may be a few seconds. But this is not a very good approach. I too had written a program with if else statement which will take each and every permutation of the 0-9 Pandigital and check for the conditions given in the qu...
Read more