Problem 18 Project Euler Solution with python

Maximum path sum I

By starting at the top of the triangle below and moving to adjacent numbers on the row below, the maximum total from top to bottom is 23.

3
7 4
2 4 6
8 5 9 3

That is, 3 + 7 + 4 + 9 = 23.
Find the maximum total from top to bottom of the triangle below:

75
95 64
17 47 82
18 35 87 10
20 04 82 47 65
19 01 23 75 03 34
88 02 77 73 07 63 67
99 65 04 28 06 16 70 92
41 41 26 56 83 40 80 70 33
41 48 72 33 47 32 37 16 94 29
53 71 44 65 25 43 91 52 97 51 14
70 11 33 28 77 73 17 78 39 68 17 57
91 71 52 38 17 14 91 43 58 50 27 29 48
63 66 04 68 89 53 67 30 73 16 69 87 40 31
04 62 98 27 23 09 70 98 73 93 38 53 60 04 23

NOTE: As there are only 16384 routes, it is possible to solve this problem by trying every route. However, Problem 67, is the same challenge with a triangle containing one-hundred rows; it cannot be solved by brute force, and requires a clever method! ;o)

As stated in the question, yes this problem has a clever way to solve. But it is very simple. The approach is dynamic programming.

Actually I found this at Stack overflow answer written by timday and answer written by mishadoff.

They both gave a very good explanation in a simple way. I will try my level best explaining the solution in my way. We are not going to consider the main problem, but the example problem for explanation.

Have a look at the following photograph:

Bottom Up Approach

Sorry for bad handwriting 😐.

I am not sure if we can call this approach bottom up approach, but I am using this term because it seemed relevant for me. Now let us understand the concept.

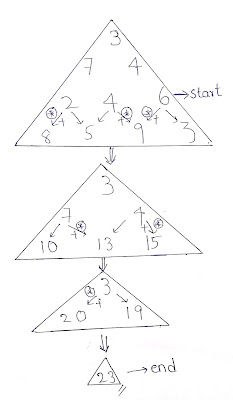
First I took the last but one row in the pyramid.

Now in the case of 2: we had option of 8 and 5. 8 has maximum value when compared to 5 and so the sum is 10.

Now for 4: 9 is better when compared to 5.

For 6: 9 is better when compared to 4.

Now the values are changed to 10(2+8), 13(4+9), 15(6+9)

Going one step further

considering 7: between 10 and 13, 13 is better.

For 4: between 13 and 15, 15 is better.

So the values change to 20(7+13), 19(4+15)

This is the final step. We have to choose between 20 and 19, in which 20 is better so the final solution will be 23.

Now you may have a  doubt that why we have chosen bottom up approach when compared to top down approach. To explain this I will consider Jeffery Sax Answer on StackOverflow.

See the following photograph and the pyramid.

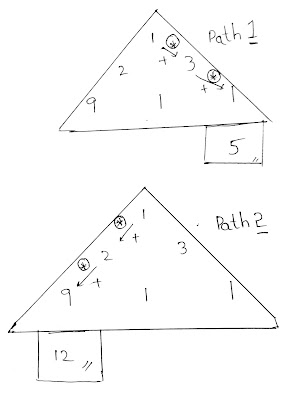
1

2 3

9 1 1

Top Down approach

Now as you can see that if we follow path 1 then we get our maximum sum as 5, but if we follow path2 then we get the sum of 12. Which one do you think is maximum?

If we were to solve this problem using bottom up approach, then we will get correct solution. See photograph if you want.

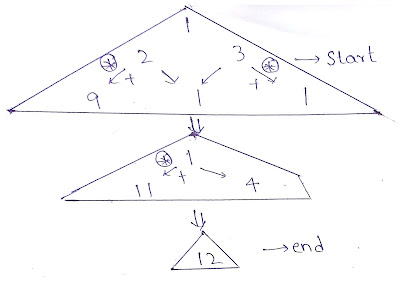Bottom up approach solution for example 2

As you can see using bottom up approach we have arrived at the correct solution.

you can also apply this concept for reverse pyramid.

I have used Bottom Up approach to solve this problem. I have also counted the number of iterations in which we have arrived at the solution and compared it with the number of iterations one would take to arrive at the solution if we were to follow all the paths.

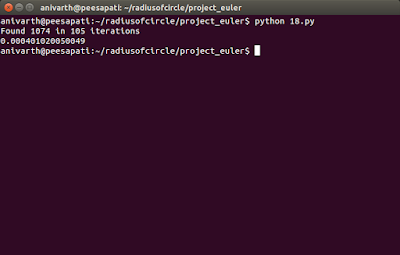
Compared to 16384 paths given in the question, my program only did 105 iterations and I have arrived at the solution. That means that using this approach I have eliminated 16279(99%) extra iterations. Also I have obtained the solution in a very small amount of run time.

Okay, by now after reading till here, I am assuming that you have understood the algorithm. Lets get into the programming part.

Program

The program which I wrote is as follows:

The code is well commented again.

You can see the execution of the algorithm which I've discussed above from Line41 in the program.

If you want to download above program then you can download it from Github Gist pep18.py

Output

Answer: 1074
Execution time: 0.000401020050049 seconds
Output:

Project Euler Problem 18 output

Project Euler Problem 18 with solution

Summary

I think this problem had a little twist. When the problem was introduced in the question it was introduced in the form of top down approach, but the wise solution was to solve the problem using bottom up approach. Anyways we have solved the problem in less than 1% iterations given in the question. So we can call this program as optimized or framing it other way performance of the program is satisfactory 😉.

I hope you enjoyed reading solution for this problem. If you have any doubt or didn't understand anything then comment in the comment box below and I will be glad to help you.

Please don't hesitate to comment if you have found any typo or you have better/different solution.

You can also contact me if you want .

Thank you. Have a nice day.😀