Problem 38 Project Euler Solution with Python

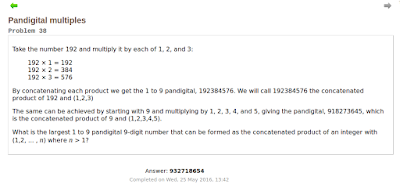
Pandigital multiples

Take the number 192 and multiply it by each of 1, 2, and 3:

192 × 1 = 192
192 × 2 = 384
192 × 3 = 576

By concatenating each product we get the 1 to 9 pandigital, 192384576. We will call 192384576 the concatenated product of 192 and (1,2,3)
The same can be achieved by starting with 9 and multiplying by 1, 2, 3, 4, and 5, giving the pandigital, 918273645, which is the concatenated product of 9 and (1,2,3,4,5).
What is the largest 1 to 9 pandigital 9-digit number that can be formed as the concatenated product of an integer with (1,2, ... , n) where n > 1?


Its been a long time since my last post, but due to some other work I was not able to post a solution. Sorry for that!

This problem(38) is very easy once you have understood the question correctly. I will first explain you the question and then I will explain you the program.

The first condition from n>1 is that you will for sure have to do iterations for a minimum of 2 times.

The question says to take an integer and multiply it with numbers from 1 to infinity until the concatenated product has length of more than 9 digits.

For example, take the number 327, Now we will start multiplying it with 1

327 x 1 = 327

As the length of the concatenated product(327) is less than 9 digits, so multiply with 2

327 x 2 = 654

Now the concatenated product is 327654, this one also has a length less than 9 digits so go for next iteration,

327 x 3 = 981

Now the concatenated product is 327654981, whose length is 9 digits so stop iteration and proceed for next decision.

Okay you might not have understood the problem correctly, so lets take an another example and see what is happening. Now consider a big number  7932, Lets again start with number 1

7932 x 1 = 7932

Concatenated product is 7932 which is not upto 9 digits, so go for next iteration

7932 x 2 = 15864

Concatenated product is 793215864 which has 9 digits and so we can stop here. 

According to the question we are not just limited to iterating it for 3 or 4 times, but we should iterate until the number of digits in the concatenated product has 9 or more digits.

After we will get the concatenated number and the first condition we check for is if the given number has 9 digits or not. If the number doesn't have 9 digits then it will not become 1-9 pandigital number.

Next we will also check if the set(given number) has only length of 9, because if the value is not equal to 9 then there are repetitions(Sets are python's unordered data structures which only have unique entries). Sometimes the problem arises with the number 0 if we are using sets. For example say the number is 0123456789, then the len(set(0123456789)) will give 9 again which is a mistake, so finally we will check if the number 0 is not in the concatenated product.(Check out a detailed example given under the program section)

 I chose 10000 as the upper limit because, if we take a 4 digit number and then multiply it with 1 we will get 4 digits. Now the concatenated product is 4 digits. As the minimum number of iterations, we will have to do is 2(n>1 so minimum 2), 4 digit number multiplied with 2 will give a minimum of 4 digits and a maximum of 5 digits. So lets assume the worst case and if we get only 4 digits, our concatenated product is 8 digits, iteration will continue for one more time and will end up with 12 digits, but if the same 4 digit number multiplied with 2, if have given a 5 digit number, the iteration will stop here.

Now consider the case of 5 digit number, for the first iteration we get 5 digits in the concatenated product, and for the second iteration we get we get a minimum of 10 digits in the concatenated product, which is not really necessary. We only need 9 digits, not more than that, not less than that. 

So finally we can say that 4 digit numbers or less, have chance of giving 9 digits but for the case of 5 digits we don't have any chance of getting 9 digits. So I have chosen the upper limit to be 10000 which will make the for loop to work till 9999.  

That's it, this is all the algorithm program has. You can see the program now, you will have a clearcut understanding of the same. Note that I have also written the explanation for the program.

Program

I have tried to maintain the PEP8 standard but would have missed a few. You can add them if you want to.
 
I will start from line 10. Here at the start of the iterations we are assuming that the value of the largest concatenated product is 0.

largest = 0

We are looping upto four digits. For each and every loop we will get a concatenated product, which at the beginning is '', As we don't know the number of iterations we will use a while loop, whose iterator will be integer. Now start the while loop, don't stop the iterations until the number of digits is less than 9.

On line 33, we are checking if the concatenated product is having length of only 9 digits, number 0 not in the string. 

And one more Boolean is  to check if the numbers are all unique, I have used len(set(mulitplication)) == 9

Lets consider the numbers 012345678, 123456789, 334857875 in the form of strings. We will apply len(set(number)) and see what will happen

>>> set('012345678')
set(['1', '0', '3', '2', '5', '4', '7', '6', '8'])
>>> len(set('012345678'))
9
>>> set('123456789')
set(['1', '3', '2', '5', '4', '7', '6', '9', '8'])
>>> len(set('123456789'))
9
>>> set('334857875')
set(['8', '3', '5', '4', '7'])
>>> len(set('334857875'))
5
>>> 

We know that sets are an unordered collection of unique objects, and so as the third number which was not pandigital(unique 9 digit number with numbers from 1-9 all present) will be eliminated.

Now both the second and first number have unique numbers in their digits and so their length is 9, but the first number is not pandigital from 1-9. Yes you have guessed it right, this is the reason why we have added an another condition to check if the number which doesn't have 0 will be qualified to be a pandigital.

Now combine all the Boolean conditions and you will for sure understand every thing clearly.

If the number will qualify the above condition of being a pandigital 1-9, 9 digit numbers then we will check if the current number(concatenated product of the iteration) is bigger than the previous value of the pandigital, then you can change the value of the largest number.

Okay lets consider an example. To be simple and realistic we will consider the number 9.

At the start of iteration, the values of
multiplication = ''
integer = 1

Now the while loop starts, the length of multiplication is 0 so,
multiplication = '9' # (9*1)
integer = 2

In the similar way, second iteration of the while loop is as follows:
multiplication = '918'
integer = 3

Now this iteration will continue six times and at the end the values are as follows:
multiplication = '918273645'
integer = 7

Now on Line 33 the boolean equations are as follows:
len(multiplication) == 9 # True
len(set(multiplication)) == 9 # True
'0' not in multiplication # True

All the others are simple.

As always you can download the source code from Github Gist pep38.py

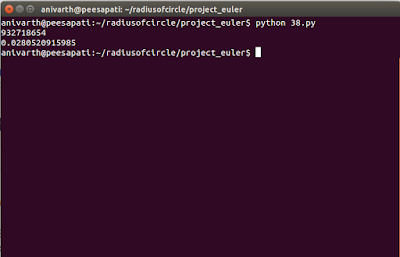
Output

Answer: 932718654
Execution time: 0.0280520915985
Output:

Project Euler Problem 38 output

Project Euler Problem 38 with answer

Summary

I had the problem of understanding the question at first. When I read the question for the third time, then it was very easy and in the first attempt, I have completed writing the program. Even though this program can be optimized a bit more to improve performance, I am satisfied with the time of execution and have not thought about that. You can try improving the program.

As always if you have any doubt or didn't understand anything then comment in the comment box below and I will be glad to help you.

Please do comment if you have found a typo or have a better program or have a different program or have a suggestion. I will be glad to view each of them.

You can also contact me.

Thank you. Have a nice day😃.