Skip to main content

Problem 41 project Euler Solution with python

Pandigital prime

We shall say that an n-digit number is pandigital if it makes use of all the digits 1 to n exactly once. For example, 2143 is a 4-digit pandigital and is also prime.
What is the largest n-digit pandigital prime that exists?
An another question on Pandigital. I have written two solutions, one solution demanded homework and the other required programming logic. Both had their own pros and cons. But I will finalize the solution which demanded the programming skills.

Anyways you can see both the programs below.

Better performing code considers the divisibility of 3. See the Answer written by engineer on Stack Overflow, you will understand the algorithm.
(Second Program I wrote) 
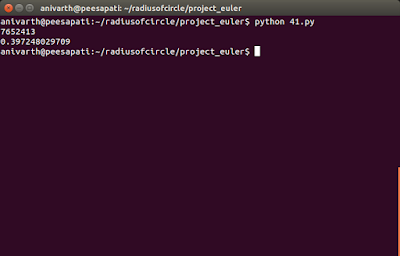
# http://radiusofcircle.blogspot.com

# importing the permutations method
from itertools import permutations

# importing time module
import time

# time at the start of program execution
start = time.time()


def is_prime(n):
    """Function to check if
    the given number is prime"""
    for i in xrange(2, int(n**0.5)+1):
        if n % i == 0:
            return False
    return True

# permutations of numbers from 1-7
p = permutations('1234567')

# for loop to loop from reverse order
# from higher to lower
for i in list(p)[::-1]:
    if int(i[6]) % 2 != 0:
        number = int(''.join(i))
        if (number+1) % 6 == 0 or (number-1) % 6 == 0:
            if is_prime(number):
                print number
                break

# time at the end of program execution
end = time.time()

# total time of execution
print end-start
This program gets executed in 0.00150895118713 seconds. But this demanded mathematics rather than more programming logic.

 I have explained most of the code in the program section.

Program

Check out itertools.permutations to understand what permutations are.

 is_prime
This is a very simple function to check if the given number is prime or not.

 Now the value of a = '123456789', which when permuted will give all the 1-9 pandigital numbers. If you don't want 1-9 pandigital and suppose say, you want only 1-7 pandigital number, then consider only a[:7].

 flag = True

 j = 0, this one is while loop iterator

 While loop is executed because the value of flag is True at the instant.

 p = permutations(a[:9]) = permutations('123456789')

 As we know that the permutations will return all the numbers arranged from small to big. As we wanted bigger prime number we will check from last to first. I have used [::-1] to reverse the given list.

 Take an element from the permutations and then check if the last element is not even.

 Next condition uses the fact that all the prime numbers are of the form 6k+1 and 6k-1 but the vice versa is not true.

 If the number passes the above test then check if it is prime. If it is prime then this will be the largest pandigital prime number because we are coming in reverse order.

 If any prime is not found in the present iteration then start checking permutations of '12345678', i.e.j = 8 = 9-1. At the end when the prime is found, print the prime number and then flag = False to stop the outer while loop and break to stop the present for loop.

Output

Summary

This problem took some time for me to complete, but I am really satisfied. I am very happy with the first program I have written because I have used a lot of logic rather than mathematics. Even though the program also had some mathematics it contained more programming logic. Second solution, a child of the first program used a very simple mathematical logic and had a better execution time. I am not happy for not getting this idea until I have seen an answer on Stack.

 As always if you have any doubt then you can comment in the comment box below.

 Please do comment if you have found any typo or have a different program or have a better program or if you have a suggestion. I will be very happy to view each of them.

 You can also contact me.

 Thank you. Have a nice day😃.
Labels: