Project Euler Problem 64 Solution with python

Odd period square roots¶

All square roots are periodic when written as continued fractions and can be written in the form:
$$ \begin{equation} \sqrt n = a_0 + \cfrac{1}{a_1 + \cfrac{1}{a_2 + \cfrac{1}{a_3 + \cfrac{1}{a_4....} } } } \end{equation} $$
For example, let us consider $\sqrt 23$:
$$ \sqrt 23 = 4 + \sqrt 23 -4 = 4 + \cfrac{1}{\cfrac{1}{\sqrt 23 - 4}} = 4 + \cfrac{1}{1 + \cfrac{\sqrt 23 - 3}{7}} $$ If we continue we would get the following expansion: $$ \begin{equation} \sqrt 23 = 4 + \cfrac{1}{1 + \cfrac{1}{3 + \cfrac{1}{1 + \cfrac{1}{8...} } } } \end{equation} $$ The process can be summarised as follows: $$ a_0 = 4, \cfrac{1}{\sqrt 23 - 4} = \cfrac{\sqrt 23 + 4}{7} = 1 + \cfrac{\sqrt 23 - 3}{7} $$ $$ a_1 = 1, \cfrac{7}{\sqrt 23 - 3} = \cfrac{7(\sqrt 23 + 3)}{14} = 3 + \cfrac{\sqrt 23 - 3}{2} $$ $$ a_2 = 3, \cfrac{2}{\sqrt 23 - 3} = \cfrac{2(\sqrt 23 + 3)}{14} = 1 + \cfrac{\sqrt 23 - 4}{7} $$ $$ a_3 = 1, \cfrac{7}{\sqrt 23 - 4} = \cfrac{7(\sqrt 23 + 4)}{7} = 8 + \sqrt 23 - 4 $$ $$ a_4 = 8, \cfrac{1}{\sqrt 23 - 4} = \cfrac{\sqrt 23 + 4}{7} = 1 + \cfrac{\sqrt 23 - 3}{2} $$ $$ a_5 = 1, \cfrac{7}{\sqrt 23 - 3} = \cfrac{7(\sqrt 23 + 3)}{14} = 3 + \cfrac{\sqrt 23 - 3}{2} $$ $$ a_6 = 3, \cfrac{2}{\sqrt 23 - 3} = \cfrac{2(\sqrt 23 + 3)}{14} = 1 + \cfrac{\sqrt 23 - 4}{7} $$ $$ a_7 = 1, \cfrac{7}{\sqrt 23 - 4} = \cfrac{7(\sqrt 23 + 4)}{7} = 8 + \sqrt 23 - 4 $$ It can be seen that the sequence is repeating. For conciseness, we use the notation √23 = [4;(1,3,1,8)], to indicate that the block (1,3,1,8) repeats indefinitely. The first ten continued fraction representations of (irrational) square roots are:
$\sqrt 2$ = [1;(2)], period=1
$\sqrt 3$ = [1;(1,2)], period=2
$\sqrt 5$ = [2;(4)], period=1
$\sqrt 6$ = [2;(2,4)], period=2
$\sqrt 7$ = [2;(1,1,1,4)], period=4
$\sqrt 8$ = [2;(1,4)], period=2
$\sqrt 10$ = [3;(6)], period=1
$\sqrt 11$ = [3;(3,6)], period=2
$\sqrt 12$ = [3;(2,6)], period=2
$\sqrt 13$ = [3;(1,1,1,1,6)], period=5

Exactly four continued fractions, for N ≤ 13, have an odd period.

How many continued fractions for N ≤ 10000 have an odd period?

Actually, this problem requires a lot of google search or you should be a mathematician who can derive formulas. I have chosen the former and found these sources: Wikipeida: Methods of computing square roots and Even & odd periods in continued fractions of square roots.
According to the second source, you will see the repetition when you will get double the value of the first number. For example, in the case of $\sqrt{13}$, the first number is 3 and the repetition will start when you will encounter double the value of the first number i.e. 6. You can check the same with other numbers also.
And according to the first source, the values of a will be:

$$ m_0 = 0\\ d_0 = 1\\ a_0 = int(\sqrt n)\\ m_{n+1} = d_n \times a_n - m_n\\ d_{n+1} = \cfrac{n - {m^{2}}_{n+1}}{d_{n}}\\ a_{n+1} = int(\cfrac{a_0 + m_{n+1}}{d_{n+1}}) $$

Based on the above formulas or algorithm we can get the solution.
But before I have solved the problem using the above algorithm I used another technique which didn't work. I am presenting you the non-working code below, so that you can use it somewhere else or just look at it for debugging.

In [1]:

# http://radiusofcircle.blogspot.com
def continued_fraction(n):
    """
    This function will calculate
    Continued fraction of a given number"""
    integer = int(n)
    decimal = n - integer
    cf_list = [integer]
    if decimal != 0:
        while integer != 2*cf_list[0]:
            decimal_inv = 1/decimal
            integer = int(decimal_inv)
            decimal = decimal_inv - integer
            cf_list.append(integer)
    return cf_list

You can download the ,py file from Github Gist pep64_f.py The algorithm is as follows:
Consider for example $\sqrt{2} = 1.414......$

• Now we will separate 1 and thus the remaining value is 0.414...
• Inverse the value of 0.414... and you will get 2.414...
• Separate 2 from 2.414.. and you will be left with 0.414...
• Till now your list of integers will be [1, 2] and this will continue.
• But as the value of 2 is 2 * 1 you can terminate the algorithm

You can read more about this algorithm from here: 6 Continued fractions for square-roots
I have changed a little bit of the code(compared to the code on my PC) so that you can use it as a function. The function will return a list.
We will try using this algorithm and for most of the values, it will give correct results.

In [2]:

# import square root from math module
from math import sqrt

# square root of 2
print continued_fraction(sqrt(2))

# square root of 13
print continued_fraction(sqrt(13))

# square root of 337 - fails
print len(continued_fraction(sqrt(337)))

[1, 2]
[3, 1, 1, 1, 1, 6]
2681

The exact value that len(continued_fraction(sqrt(337))) should return is [18,2,1,3,1,11,2,4,1,3,3,1,4,2,11,1,3,1,2,36]. You can check it from here: Continued Fraction calculator
As you can see that the algorithm used above will not give you correct results at some points on the number line. For that matter, using this algorithm we will get 3000+ numbers below 10,000 whose continued fractions have odd periods.
Even though we haven't used the above function, an insight will help. Below is the real program that I have used to find the solution.

Program¶

In [ ]:

# http://radiusofcircle.blogspot.com

#import time
import time

# square root function
from math import sqrt

# time at the start of program execution
start = time.time()

# function to calculate the continued fraction
def cf(n):
    mn = 0.0
    dn = 1.0
    a0 = int(sqrt(n))
    an = int(sqrt(n))
    period = 0
    if a0 != sqrt(n):
        while an != 2*a0:
            mn = dn*an - mn
            dn = (n - mn**2)/dn
            an = int((a0 + mn)/dn)
            period += 1
    return period

# counter
counter = 0

# for loop from 0 to 10000
for i in xrange(10000):
    if cf(i) % 2 != 0:
        counter += 1

# number of instances
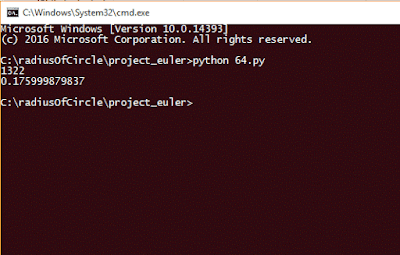
print counter

# time at the end of program execution
end = time.time()

# total time taken to run the program
print end - start

This program is pretty simple. I have converted the formulas given above into a python program.
You can download the program from Github Gist pep64.py.

Output¶

Answer: 1322
Execution time: 0.17599987 seconds
Output:

Project Euler Problem 64 solution with python

Project Euler Problem 64 along with answer

Summary¶

This problem was not easy until I found the source on Wikipedia. I used the first program to find the solution and kept on trying for the solution with no results. First of all, I didn't understand why I was not able to get the answer with the given function. This function maliciously gave correct results for numbers up to 100. After a lot of trials I was able to find the wiki source and finally got the solution. I am satisfied with the program because it is executing in less than 1 second.
As always, if you have any doubt comment in the comment box below and I will be glad to help you.
If you have a better program or a different approach or have feedback please comment in the comment box and I will be very happy to see your comment.
You can also contact me.
Thank you. Have a nice day😃.